Posts
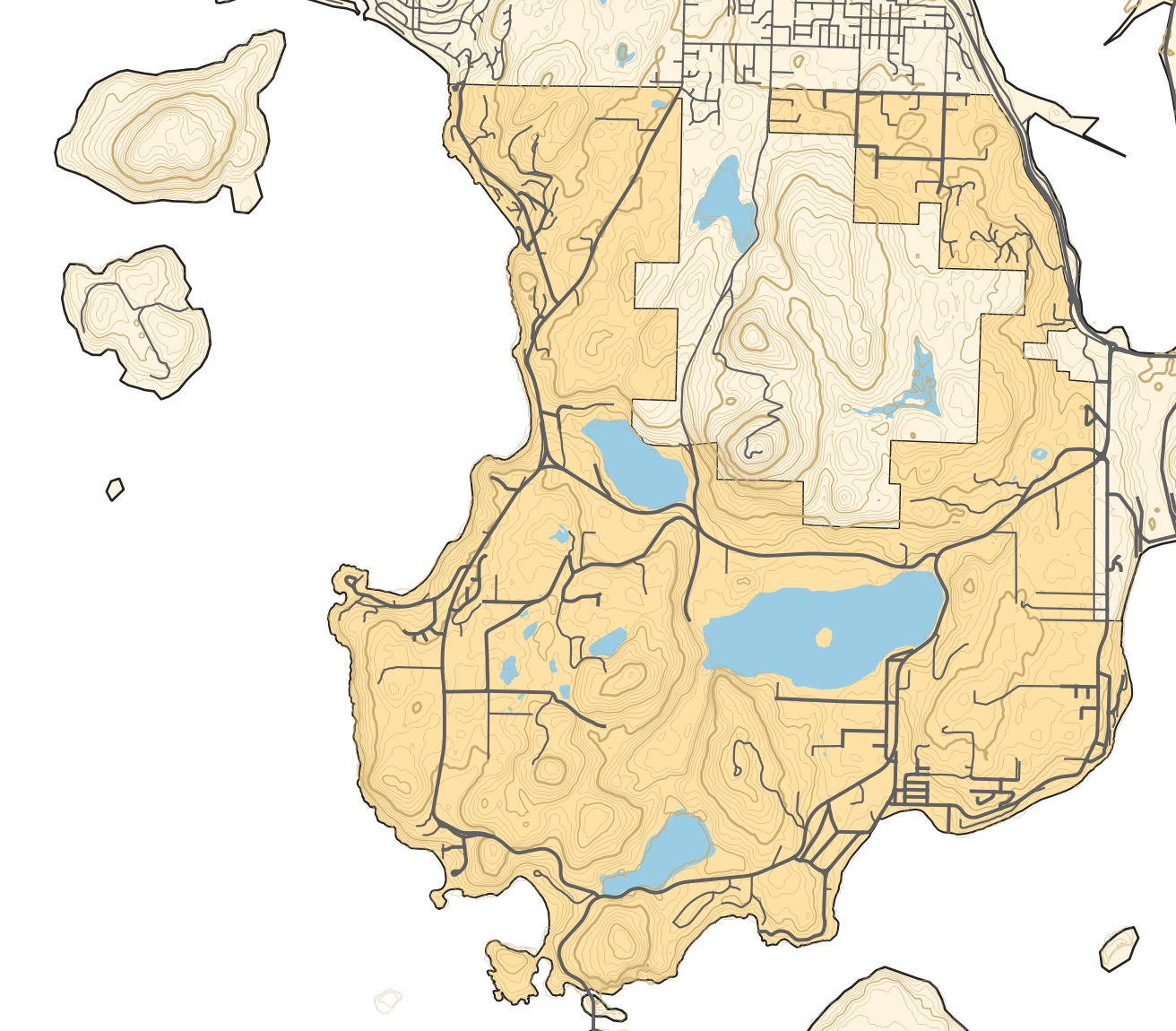
Working with basic topography data
You could perhaps tell from some previous posts that I'm a bit of a geospatial data nerd. In keeping with that, for several years I've been searching on and off for reliable sources of elevation/topographic data. This week, at long last, I think my search can be over.
The short version: You can download elevation data from NASA's Shuttle Radar Topography Mission and then generate contour lines from that.
Turbulent flow in hoses
Yet another pump operations/water flow post, sorry folks! If only it weren't so darn interesting...
This is another "Zeph convinces themself that the book is right" post, this time on a statement about laminar versus turbulent flow in hoses:
The pressures in hose are typically high enough to cause turbulent flow.
If you're interested in a demonstration of this, buckle in and come along! If not, might I suggest different reading material?
Hydrant capacity calculations
Yet another post on pump operations, sorry y'all. This one, like a previous post, is me coming to terms with a statement about water flow in a textbook. This time around, I'm looking at how to estimate additional hydrant capacity if you're already flowing some amount of water from your hydrant.
Big picture, I'll do some calculations based on Bernoulli's equation to show how much additional water flow a hydrant can provide, then I'll briefly compare that to two of the three methods discussed in Sykes and Sturtevant's 1999 Fire Apparatus Operator: Pumper textbook.
Ways of viewing pressure
Well, guess who's still making sense of water flow through hose and pumps these days? (Yep, you got it. It's me.)
Today I finally figured out a point of confusion I'd had for weeks around the relationship between pressure and volume of flow out of a nozzle. Turns out the answer has to do with a new-to-me way of viewing pressure that offers some additional tools for reasoning about how water flow works.
Head pressure
Head pressure is the pressure created by a difference in height between where water is coming from and a discharge. It's important for things like how much pressure you'll get from a hydrant or how much pressure you lose if you're pumping up a steep driveway. If you read a textbook, it'll say something like
To convert head in feet to head pressure in psi, divide the number of feet by 2.304.
This is me proving to myself that that works. (Spoiler alert: it does.)