Head pressure

28 August, 2022, 5 min, 900 words

Tags: fire-stuff physics

Head pressure is the pressure created by a difference in height between where water is coming from and a discharge. It's important for things like how much pressure you'll get from a hydrant or how much pressure you lose if you're pumping up a steep driveway. If you read a textbook, it'll say something like

To convert head in feet to head pressure in psi, divide the number of feet by 2.304.

This is me proving to myself that that works. (Spoiler alert: it does.)

So, we're going to start with the same simplification I made last time by converting a reservoir and some complex series of pipes into a single vertical stack of water. I've convinced myself that this will result in the same discharge pressure, though articulating why is still hard. Here's what the simplification looks like, though:

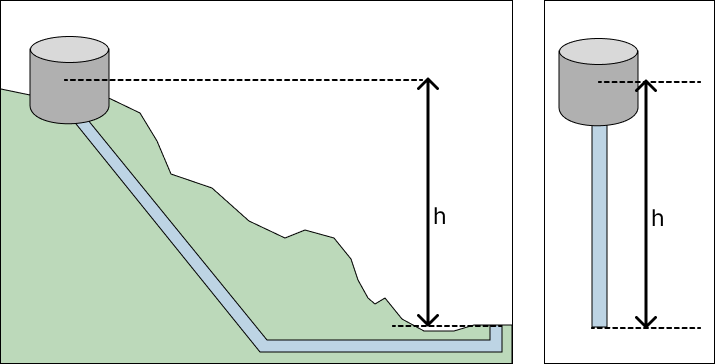
Okay, so given $h$, we want to calculate the pressure at the bottom of this tube. Awesome. Let's start with the easy stuff.

Let's say the cross-sectional area of the tube is $A$. Then the volume of water contained in the tube is:

$$ V = h\cdot A $$

If the density of water is $\rho$, then the mass of this water is:

$$ m = V\cdot\rho = h\cdot A\cdot\rho $$

(Note: I will use italicised $m$ for mass, and a non-italicized $\text{m}$ for meters. This is more generally true – units here will be non-italicized, while variables will look like variables.)

Okay, and the force resulting from all this water pushed down by gravity will be $F=mg$, or

$$ F = h\cdot A\cdot\rho\cdot g $$

Finally, pressure is force per area. So the pressure at the bottom of the tube is

$$ P = \frac{F}{A} = h\cdot\rho\cdot g $$

(Thank goodness, the cross-section of the tube doesn't matter.)

A quick note on the units of pressure. In SI units, pressure is measured in Pascals, which are Newtons per square meter:

$$ 1\ \text{Pa}=1\frac{\text{N}}{\text{m}^2}=1\frac{\frac{\text{kg}\cdot\text{m}}{\text{s}^2}}{\text{m}^2} =1\frac{\text{kg}}{\text{m}\ \text{s}^2} $$

In imperial units, pressure is measured in pounds per square inch (psi). Or, more properly, in pounds-force per square inch. (Pet peeve: anything to do with a system where "pounds" can mean two wildly different things with different units and that don't actually convert between each other with any simple/memorable conversion factor.)

Substituting in values for water's density and the acceleration due to the Earth's gravity:

\begin{align} P &= h\rho g\\ &= h\cdot\frac{1\ \text{kg}} {1000\ \text{cm}^3}\cdot\left(9.81\ \frac{\text{m}}{\text{s}^2}\right) \end{align}

We're now going to multiply our pressure by one in many different forms to convert from imperial units (feet) to SI and then back to imperial.

\begin{align} P &= h\rho g\\ &= h\cdot\frac{1\ \text{kg}} {1000\ \text{cm}^3}\cdot\left(9.81\ \frac{\text{m}}{\text{s}^2}\right)\\ &= h\cdot\frac{1\ \text{kg}} {1000\ \text{cm}^3}\cdot\left(9.81\ \frac{\text{m}}{\text{s}^2}\right) \cdot\left(\frac{100\ \text{cm}}{1\ \text{m}}\right)^3\\ &= h\cdot9,800\cdot\frac{\text{kg}\cdot\text{m}}{\text{m}^3\ \text{s}^2}\\ &= \frac{h}{\text{m}}\cdot 9,800\cdot\frac{\text{kg}}{\text{m}\ \text{s}^2}\\ &= \frac{h}{\text{m}}\cdot 9,800\cdot\text{Pa} \end{align}

Note that the units still work – as long as $h$ has a length-like dimension (say, feet or meters), we end with a unit of pressure, phew! Now back to psi:

\begin{align} P &= \frac{h}{\text{m}}\cdot 9,800\cdot\text{Pa}\\ &= \frac{h}{\text{m}}\cdot 9,800\ \frac{\text{N}}{\text{m}^2} \cdot\left(\frac{1\ \text{ft}}{12\ \text{in}}\cdot \frac{1\ \text{m}}{3.3\ \text{ft}}\right)^2\\ &= \frac{h}{\text{m}}\cdot 6.3\ \frac{\text{N}}{\text{in}^2}\\ &= \frac{h}{\text{m}}\cdot 6.3\ \frac{\text{N}}{\text{in}^2} \cdot\frac{1\ \text{lbf}}{4.45\ \text{N}}\\ &= \frac{h}{\text{m}}\cdot 1.4\ \frac{\text{lbf}}{\text{in}^2}\\ &= \frac{h}{\text{m}}\cdot 1.4\ \text{psi}\\ &= \frac{h}{\text{m}}\cdot\frac{1\ \text{m}}{3.3\ \text{ft}}\cdot 1.4\ \text{psi}\\ &= \frac{h}{\text{ft}}\cdot 0.4\ \text{psi}\\ &= \frac{h}{\text{ft}}\cdot\frac{1}{2.3}\ \text{psi} \end{align}

And would you look at that! If you have a height difference of, say 100 feet, then $h/\text{ft}$ is 100, and your resulting head pressure is $100/2.3\ \text{psi} = 43\ \text{psi}$.

As a side note, because everything is better in SI units, when it comes to a head measured in meters, you can convert to kPa by just multiplying the height (in meters) by ten. #SIforlife

(Is this likely to be useful to anyone but me? No. Too bad. My blog, my rules.)