Optimization in c++
, 4 min, 668 words
Tags: programming
Recently, a question arose about the most efficient way to store certain data in a program. In essence, a unique identification is needed for a detector component, which can be broken down into properties A, B, C, and D. Many of these things will need to be initialized, stored, and sorted, and we wanted to know if a c++ struct (essentially identical to a c++ class, but conventionally used for storing related information together; at least in my experience, they tend to have far fewer methods and their fields are almost entirely public) or a sort of hashed integer (multiply property A by 10000, add B times 1000, etc.) would be more efficient. A struct can have a manual comparison function, so it would be sortable, but we were interested in determining how efficient this sorting process is compared to sorting plain old integers, so I ran a quick little study to compare them.
The three candidate data structures are:
- An integer, which is defined as $(A×10000)+(B×1000)+(C×100)+D$. The sorting function is a simple comparison, but is provided manually in order to ensure similarity between the trials.
- A Specification struct, which contains fields for track number, view, plane, and wire, with a comparison function that accesses one or more of these fields in order, henceforth known as the naive struct.
- A Specification struct with the same fields as above, but with an additional integer uniqueID field, calculated after all setting is done according to the formula above. The sorting function compares only the uniqueID. This type is referred to as the smart struct.
What I investigated was the execution time to create and sort $10^7$ objects of these different data types, using c++'s clock type and clock() method to count CPU cycles spent in the program (so as to avoid influences from system interruptions).
I timed both creation and sorting the data structures with no optimization
and then with gcc -O3 optimization. Results are summarized in the figures
below, and discussion is below the relevant figure.'
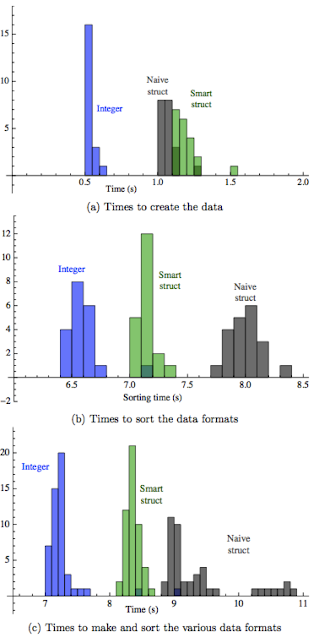
Here, unsurprisingly, we see that the integer is faster in all respects than the structs. Since we have a total of $10^7$ objects, the total time difference boils down to around 150 nanoseconds per object of extra time. As we would expect, it takes a little longer to create the smart struct than the naive one, since we have to set up the uniqueID, but it sorts much faster. The interesting stuff starts to happen when the code is compiled with maximum (standards-compliant) optimization.

For one thing, it's obvious that optimization speeds up the code, especially the sorting, by a lot: it runs around a factor of four faster than in the unoptimized version. It also brings the performance of the three data structures much closer together, and for some strange reason, the smart struct appears to actually sort faster than the integers; what a mystery!
The last consideration is what I call the bare integers; that is, the same uniqueID as held by the regular integers, but with the default integer sorting mechanisms, rather than a custom-provided function. The running time difference between the bare and bloated integer types is on the order of 20 nanoseconds, which corresponds to around 40 assembly instructions; probably around the right number to correspond to a function call.
My conclusion from this study is that when compiled with optimization, structs and ints are roughly identical in terms of CPU time required to create and sort them. Since structs pretty dramatically increase readability of the code, I'm sticking with those instead of tiptoeing around a funky hashed integer.