Neutrino Astrophysics: Neutrino oscillations
, 4 min, 617 words
Tags: physics neutrinos particle-physics
When last we left our heroes, the Sudbury Solar Neutrino Observatory (SNO) had concluded that while predictions for the total flux of neutrinos at the Earth were accurate, only about a third of those that reach us are electron neutrinos. This naturally begs the question: what are the rest of them?
Subsequent experiments, using both astrophysical and accelerator neutrinos, concluded that they oscillated into muon- and tau-flavored neutrinos. This process is highly analogous to strangeness oscillations in the neutral kaons I've written so much about. In essence, neutrinos are produced and interact in flavor eigenstates, as the electron neutrino $\nu_e$, the muon neutrino $\nu_\mu$, and the tau neutrino $\nu_\tau$, but propagate through space in mass eigenstates creatively named $\nu_1$, $\nu_2$, and $\nu_3$. Since these particles have distinct masses, they also have distinct time evolution, and based on oscillation frequencies, we can determine the mass differences between various eigenstates.
Unlike in the kaon system, however, in which the $K^0$ had an equal probability of being a $K_1$ compared to a $K_2$, it turns out the $\nu_e$ is much more likely to be a $\nu_1$ than any other mass eigenstate, so in order to describe the probabilities associated with converting between the two bases, we have to introduce the concept of mixing angles. For simplicity, let's just look at two of the three neutrino types in both bases: $\nu_e$ and $\nu_\mu$ for the flavor eigenstates and $\nu_1$ and $\nu_2$ for the mass eigenstates. We could choose two constants to represent the components of $\nu_e$ in the two mass eigenstates, but in order to ensure normalization, we instead use the sine and cosine of an angle, $\theta_{12}$, and end up with \begin{align} \nu_e &= \cos(\theta_{12})\nu_1 + \sin(\theta_{12})\nu_2\\ \nu_\mu &= -\sin(\theta_{12})\nu_1 + \cos(\theta_{12})\nu_2 \end{align} We can similarly convert from the mass eigenstates to the flavor eigenstates. Throwing in a third state complicates matters somewhat: we have to add two new mixing angles in order to describe the pairwise relationship between the states, and also have to add what's called a CP violating phase $\delta$. Overall, the relationship is a little messy:
$$ \left(\begin{array}{c}\nu_e\\ \nu_\mu\\ \nu_\tau \end{array}\right)= \left(\begin{array}{ccc} c_{12}c_{13} & s_{12}c_{13} & s_{13}e^{-i\delta}\\ -s_{12}c_{23}-c_{12}s_{23}s_{13}e^{i\delta} & c_{12}c_{23}-s_{12}s_{23}s_{13}e^{i\delta} & s_{23}c_{13}\\ s_{12}s_{23}-c_{12}c_{23}s_{13}e^{i\delta} & -c_{12}s_{23}-s_{12}c_{23}s_{13}e^{i\delta} & c_{23}c_{13} \end{array}\right)\left(\begin{array}{c}\nu_1\\ \nu_2\\ \nu_3 \end{array}\right) $$
And if that weren't crazy enough, the matrix above uses shorthand: $c_{ij}=\cos(\theta_{ij})$ and $s_{ij}=\sin(\theta_{ij})$. If you set these equations in motion and let time run for a bit, you find that an initial electron neutrino, like one produced in the sun, propagates like this:
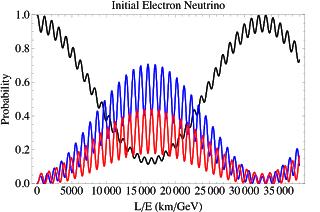
There are periods of time during which it is far more likely to detect this neutrino as a muon or tau neutrino than as an electron-flavored one! This explains the deficit of electron neutrinos observed from the sun, and relieved (astro)physicists of much distress.
This is the fourth post in a series on neutrino astrophysics. Other neutrino-related posts can be found here.