Neutrino Astrophysics: Cosmic neutrino background
, 3 min, 573 words
Tags: physics neutrinos astrophysics
Once upon a time, almost 14 billion years ago, there was a Big Bang. In the milliseconds afterwards, everything in the Universe (mostly electrons, positrons, photons, and neutrinos) was in thermal equilibrium. What that means is that the reaction $$ \nu+\overline{\nu}\leftrightarrow e^+ + e^- $$ could occur in both directions. That means the energy of the neutrinos has to be high enough to produce two more massive particles, and the cross section for the interaction has to do with the temperature of the Universe. At a temperature of around $10^{10}$ K, the temperature of the Universe dropped below the critical temperature for the reaction shown above to proceed in both directions, so neutrinos could fly free through the Universe without having to worry about interacting with much else. These neutrinos play a role in things like the ratio of protons to neutrons and the frequency components of the cosmic microwave background, and we believe that they are still around to this day. They're called the cosmic neutrino background. While general relativity is needed to understand the time evolution of the neutrino background, essentially what happens is that the neutrinos cool as the Universe expands. Theorists predict the current energy of the neutrinos in this background to be around $10^{-4}$ eV. To fully appreciate how cold these guys are, let's take another look at our favorite neutrino-related graph, the one showing flux vs. energy of neutrinos produced in hydrogen fusion.
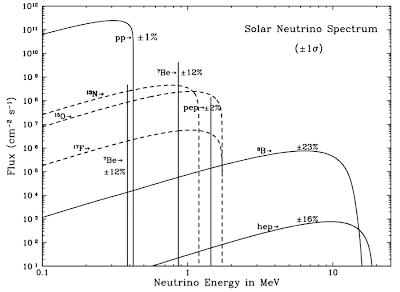
Note that the neutrinos we were so excited to detect with gallium detectors have energies around 0.3 mega electron volts. So the detection of the cosmic neutrino background is, for the time being, an insurmountable experimental challenge.
Even though we can't directly see the neutrino background, we have some good reasons to believe that it exists. For one thing, the presence of neutrinos affects the ratio of protons to neutrons, based on reactions like the following: $$ n\leftrightarrow p+e^-+\overline\nu_e\\ $$ $$ p+e^-\leftrightarrow n + \nu_e $$ As such, the presence of neutrinos throughout the Universe has dramatic effects on nucleosynthesis, the process by which nucleons combine into larger nuclei, and the current abundances give indirect evidence for the cosmic neutrino background. For another thing, apparently the angular frequency components of the cosmic microwave background's temperature fluctuations are "damped" relative to predictions in the absence of the neutrino background. I believe that has to do with the way in which vibrations propagate through the very early Universe. Neutrinos provided a certain amount of diffusion, which served to make the Universe more isotropic than it would have been in their absence.
Why do we care about this? We know very little about the early stages of the Universe's evolution. Some of our most useful information comes from observations of the cosmic microwave background, which decoupled from the rest of matter when the Universe was around 300 years old. The neutrino background, if detected, can tell us quite a bit about the intervening time period, which gets us that much closer to understanding the highest-energy event in the history of the Universe.
This is the sixth post in a series on neutrino astrophysics. Other neutrino-related posts can be found here.